- Контрольная работа по дисциплине «Материаловедение»
- Лабораторная работа по дисциплине «Материаловедение. Технология конструкционных материалов». Анализ диаграммы состояния сплавов системы "железо - углерод" в равновесном состоянии
- Контрольная работа по теплотехнике №1
- Контрольная работа по теплотехнике №2
- Контрольная работа по теплотехнике №3
- Контрольная работа по теоретической механике
- Расчетно-графическое задание №1 по статике
- Расчетно-графическое задание №2 по статике
- Контрольная работа по инженерной и компьютерной графике (1 вариант)
- Контрольная работа по сопротивлению материалов
Контрольная работа по дисциплине «Материаловедение»; 13 стр.
1) Каковы механические свойства и содержание углерода в перлите, ледебурите и цементите? Покажите на диаграмме "Железо - Углерод" места расположения чистого перлита, ледебурита и цементита. Укажите характеристики указанных структур.
2) Опишите состав и свойства марганцовистых сталей. Приведите примеры приведения высокомарганцовистых сталей в тракторостроении и обоснуйте их использование.
3) Приведите современную классификацию видов термической обработки. Поясните назначение каждого вида.
4) Приведите и опишите классификацию и маркировку электродов для ручной дуговой сварки.
Цена: 300 руб.
Лабораторная работа по дисциплине «Материаловедение. Технология конструкционных материалов». Анализ диаграммы состояния сплавов системы "железо - углерод" в равновесном состоянии; 8 стр.
Цель работы: научиться определять основные фазы и структурные составляющие; изучить превращения, происходящие в сплавах системы "железо – углерод".
Лабораторное задание
1. Дать описание фаз и структурных составляющих углеродистых сплавов с указанием в них содержания углерода и механических свойств (твердость, прочность, пластичность).
2. Вычертить диаграмму "железо-углерод" и указать на ней фазы и структурные составляющие.
3. Проанализировать характер превращения и построить кривые охлаждения для сплавов с содержанием углерода: 0,8% и 3,5%.
4. На кривой охлаждения указать фазовые превращения для каждого участка температур.
Цена: 500 руб.
Контрольная работа по теплотехнике №1; 13 стр.
ЗАДАЧА №1
Условие задачи. Для идеального цикла ДВС определить параметры характерных точек, количества подведенной и отведенной теплоты, термический к.п.д., полезную работу цикла, среднее индикаторное давление, построить на «миллиметровке» в масштабе этот цикл в координатах PV и TS.
Указания. Расчет провести без учета зависимости теплоемкости от температуры, рабочее тело – воздух, расчет провести для 1 кг, Cp=1 кДж/кг*К, t1 и Р1 – соответственно температура и давление в начале сжатия.
Исходные данные: ρ=1,3; λ=1; ε=12; t1=100°С; Р1=0,1 МПа
ЗАДАЧА №2
Условие задачи. Водяной пар с начальным давлением Р1=10 МПа и степенью сухости Х1=0.9 поступает в пароперегреватель, где его температура повышается на Δt; после перегревателя пар изоэнтропно расширяется в турбине до давления Р3. Определить (по is-диаграмме) количество тепла (на 1 кг пара), подведенное в параперегревателе, работу цикла Ренкина и степень сухости пара Х3 в конце расширения. Определить также термический к.п.д. цикла и удельный расход пара.
Исходные данные: Δt=240°C; P3=4,5
ЗАДАЧА №3
Условие задачи. Газ с начальными постоянными давлением Р1 и температурой t1 вытекает в среду с давлением Р2 через суживающееся сопло, площадь поперечного сечения которого f. Определить теоретическую скорость адиабатного истечения газа и секундный расход.
Исходные данные. N2; Р1=8 МПа; t1=20°C; Р2=4,5 МПа; f=14 мм2
ЗАДАЧА №4
Условие задачи. По горизонтально расположенной стальной трубе ![]() со скоростью ω течет вода, имеющая температуру tв. Снаружи труба охлаждается окружающим воздухом, температура которого tвозд, а давление 0.1 МПа. Определить коэффициенты теплоотдачи α1 и α2 соответственно от воды к стенке трубы и от стенки трубы к воздуху, а также коэффициент теплопередачи К, если внутренний диаметр трубы равен d1, а внешний d2.
со скоростью ω течет вода, имеющая температуру tв. Снаружи труба охлаждается окружающим воздухом, температура которого tвозд, а давление 0.1 МПа. Определить коэффициенты теплоотдачи α1 и α2 соответственно от воды к стенке трубы и от стенки трубы к воздуху, а также коэффициент теплопередачи К, если внутренний диаметр трубы равен d1, а внешний d2.
Указание. При определении α2 принять температуру наружной поверхности трубы t2 равной температуре воды.
Исходные данные. tв=160°C; ω=1,9 м/с; tвозд=14°С; d1=170 мм; d2=190 мм.
ЗАДАЧА №5
Условие задачи. Определить поверхность нагрева рекуперативного газовоздушного теплообменника при прямоточной и противоточной схемах движения теплоносителей, если объемный расход нагреваемого воздуха при нормальных условиях Vн, средний коэффициент теплопередачи от продуктов сгорания к воздуху К, начальные и конечные температуры продуктов сгорания и воздуха соответственно равны t1’, t1’’, t2’, t2’’. Начертить графики изменения температур теплоносителей для обоих случаев.
Исходные данные: Vн=2000 м3/ч; К=19 Вт/(м2·К); t1’=750°C; t1’’=550°C; t2’=18°C; t2’’= 450°C
Цена: 1000 руб.
Контрольная работа по теплотехнике №2; 13 стр.
Теоретические вопросы
Вопрос №1
Как доказать, что количество тепла Q есть функция процесса, а не состояния тела?
Вопрос №2
Выведите уравнение для вычисления изменения внутренней энергии газа, подчиняющегося уравнению состояния Ван-дер-Ваальса.
Задачи
Задача №1
В помещении компрессорной станции объемом V произошла разгерметизация трубопровода, по которому транспортируется горючий газ под давлением P1 при температуре Т1 через образовавшееся в трубопроводе сквозное отверстие площадью f газ выходит в помещение.
Рассчитать, через какое время τ во всем объеме компрессорной станции может образоваться взрывоопасная смесь, а также среднюю молекулярную массу, плотность, удельный объем и изобарную удельную массовую теплоемкость смеси, если ее температура Т=293К, а давление Р = 100 кПа. Коэффициент расхода отверстия ξ = 0,7. воздухообмен не учитывается.
Дано: Р1=1 МПа, Т1=250К, V=0.4 м3, f=5·10-4 м2, вещество - этилен.
Задача №2
Рукавная линия диаметром d=60 мм поперечно обдувается воздухом со скоростью ωв=3 м/с. Температура воздуха tв=-30 С. По рукавной линии со скоростью ωж=3.8 м/с движется вода, температура которой на входе в рукавную линию t'ж=6 С. Рассчитать максимальную длину рукавной линии из условия, чтобы температура на выходе из рукавной линии была t''ж ≥ 10С. Толщина стенки рукавной линии δ = 4мм. эквивалентный коэффициент теплопроводности материала рукава принять λ = 0,115 Вт/(м∙К).
Задача №3
Определить минимальное расстояние, обеспечивающее безопасность соседнего с горящим объекта, при исходных данных: проекция факела пламени горящего объекта имеет прямоугольную форму размером d=l=12 м, его температура Тф=1400 К, а степень черноты εф=0.6. На поверхности не горящего объекта: допустимое значение температуры Тдоп=680 К, допустимое значение плотности теплового потока (критическая плотность) qкр=12000 Вт/м2, степень черноты поверхности ε=0.85.
Кроме того, оценить безопасное расстояние от факела для личного состава, работающего на пожаре без средств защиты, от теплового воздействия при условии: а) кратковременного пребывания; б) длительной работы. При кратковременном тепловом воздействии для кожи человека qкр = 1120 Вт/м2, при длительном qкр = 560 Вт/м2. При решении задачи учитывать только теплообмен излучением. Коэффициент безопасности принять равным β=1.4.
=========================
Примечание: работа выполнена со значениями для варианта №42.
Имеется работа для варианта №45.
Теоретические вопросы:
1) Может ли энтропия системы убывать в необратимых процессах?
2) Покажите на диаграмме T-S энтальпию перегретого пара.
Данные для задачи №1
Дано: Р1=1 МПа, Т1=250К, V=0.4 м3, f=4,1·10-4 м2, вещество - этилен.
Данные для задачи №2
Рукавная линия диаметром d=60 мм поперечно обдувается воздухом со скоростью ωв=6 м/с. Температура воздуха tв=-40 С. По рукавной линии со скоростью ωж=3.8 м/с движется вода, температура которой на входе в рукавную линию t'ж=6 С. Рассчитать максимальную длину рукавной линии из условия, чтобы температура на выходе из рукавной линии была t''ж ≥ 10С. Толщина стенки рукавной линии δ = 4мм. эквивалентный коэффициент теплопроводности материала рукава принять λ = 0,115 Вт/(м∙К).
Данные для задачи №3
Определить минимальное расстояние, обеспечивающее безопасность соседнего с горящим объекта, при исходных данных: проекция факела пламени горящего объекта имеет прямоугольную форму размером d=18 м, l=12 м, его температура Тф=1400 К, а степень черноты εф=0.6. На поверхности не горящего объекта: допустимое значение температуры Тдоп=680 К, допустимое значение плотности теплового потока (критическая плотность) qкр=12000 Вт/м2, степень черноты поверхности ε=0.6.
Кроме того, оценить безопасное расстояние от факела для личного состава, работающего на пожаре без средств защиты, от теплового воздействия при условии: а) кратковременного пребывания; б) длительной работы. При кратковременном тепловом воздействии для кожи человека qкр = 1120 Вт/м2, при длительном qкр = 560 Вт/м2. При решении задачи учитывать только теплообмен излучением. Коэффициент безопасности принять равным β=1.4.
Цена: 750 руб.
Контрольная работа по теплотехнике №3; 13 стр.
Теоретические вопросы
Вопрос №1
Изобразите на диаграммах P-V и T-S графики, соответствующие изотермическому, изобарическому и изохорическому процессам вещества, свойства которого описываются уравнением Ван-дер-Ваальса.
Вопрос №2
Почему в расчётах с влажным воздухом энтальпию его всегда относят к 1 кг сухого воздуха?
Задачи
Задача №1. Температурный режим при пожаре в помещении
Производство, связанное с обращением ГЖ, размещено в помещении размерами в плане a*b, м и высотой Н, м. при аварии технологических аппаратов возможны и розлив жидкости на пол и возникновение пожара. Предусмотрены устройства, ограничивающие растекание жидкости на полу на площади квадрата f, м2 расстояние от границы горения до стены с оконными и дверными проемами, через которые будет происходить газообмен при пожаре в помещении с внешней средой, l, м .
Механическая вентиляция при возникновении пожара выключается. За счет естественного газообмена в помещение поступает такое количество воздуха, что на 1 кг горящей жидкости в среднем приходится VА, м3 воздуха.
Рассчитайте возможную температуру среды в помещении при возникновении пожара:
а) среднеобъемную через 5, 15 и 30 мин его развития;
б) локальную в точке над факелом под перекрытием через 5, 15 и 30 мин его развития;
в) локальную в точках, находящихся на высоте 1,5 м от пола и расстояниях от границы горения 0,25 l, 0,5 l, 0.75 l и l, через 2 мин его развития.
Постройте графики:
а) изменения среднеобъемной температуры среды в помещении при пожаре во времени;
б) изменения температуры среды в точке над факелом под перекрытием во времени;
в) изменения температуры среды на высоте 1,5 м в зависимости от расстояния от границы горения для 2 мин развития пожара.
По графику установите, на каком расстоянии от выхода значение температуры среды достигает 700С.
Исходные данные для выполнения расчета приведены в таблице 1.
Таблица 1
Последняя цифра шифра | 2 |
a, м b, м H, м l, м | 46 72 15 32 |
Предпоследняя цифра шифра | 4 |
f, м2 VА, м3/кг | 64 12 |
Жидкость | Толуол |
Задача №2. Нестационарная теплопроводность. Изменяющиеся граничные условия 3 рода
Рассчитайте температурное поле по толщине перекрытия через 0,5 ч после начала пожара, используя полученные при решении задачи 1 результаты расчета температуры среды над факелом под перекрытием (график изменения температуры среды под перекрытием). Перекрытие представляет собой сплошную железобетонную плиту толщиной 18 см. Толщина слоя бетона λ = 1,2 Вт/(м∙К). Начальная температура перекрытия 200С, такую же температуру имеет воздух над перекрытием.
Задачу решить методом конечных разностей графически.
Задача №3. Нестационарная теплопроводность. Не изменяющиеся граничные условия 3 рода.
Железобетонная плита перекрытия толщиной δ обогревается с одной стороны средой с температурой tг в течение τ мин. Коэффициент теплообмена на обогреваемой поверхности плиты α=11,63 е0,0023tг. Начальная температура перекрытия t0 = 200C. Коэффициент теплопроводности железобетона λ = 1,2 Вт/(м∙К), коэффициент температуропроводности а = 5,6∙10-7 м2/с.
Рассчитать температуру на расстоянии s от обогреваемой поверхности плиты: а) принимая перекрытие за неограниченную пластину; б) принимая перекрытие, как полуограниченное тело.
Данные, необходимые для расчетов, приведены в таблице 2.
Таблица 2
Последняя цифра шифра | 2 |
δ, м s, м | 0,20 0,03 |
Предпоследняя цифра шифра | 4 |
tг,0С τ, мин | 1000 50 |
=================
Примечание: работа выполнена со значениями для варианта №42.
Имеется работа для варианта №45.
Теоретические вопросы:
1) Как определить v’ и v”для вычисления внутренней энергии влажного пара по формуле Uk = v’ (1 – X) + v” X ?
2) Напишите выражение закона действующих масс для следующих реакций:С+СО2<=>2CO и СО+H2O<=>CO2+H2
Исходные данные для задачи №1
Последняя цифра шифра | 5 |
a, м b, м H, м l, м | 52 54 9 25 |
Предпоследняя цифра шифра | 4 |
f, м2 VА, м3/кг | 64 12 |
Жидкость | Толуол |
Исходные данные для задачи №3
Последняя цифра шифра | 5 |
δ, м s, м | 0,30 0,08 |
Предпоследняя цифра шифра | 5 |
tг,0С τ, мин | 1100 50 |
Цена: 800 руб.
Контрольная работа по теоретической механике; 37 стр.
Задача C1. Равновесие рамы под действием произвольной плоской системы сил
Условие. 11а жесткую раму, закрепленную в точке А шарнирно, а в точке В прикрепленную или к невесомому стержню или к шарнирной опоре на катках (стержень прикреплен к раме и к неподвижной опоре шарнирами), действуют: сосредоточенные силы ![]() пара сил с моментом M и распределенная нагрузка интенсивностью q.
пара сил с моментом M и распределенная нагрузка интенсивностью q.
Определить реакции опор, пренебрегая весом рамы и стержней (рис. С1.1, табл. С4).

Рис. С1.1

Табл. С4
Задача С2. Центр тяжести. Равновесие составной конструкции под действием произвольной плоской системы сил
Условие. Составная конструкция, состоит из однородной плиты сложного сечения ADB веса G и невесомой части BE. Способ соединения конструкции - шарнир В. Конструкция может быть закреплена с помощью шарниров, невесомых стержней, шарнирной опоры на катках, свободного опирания или жесткой заделки. На конструкцию кроме силы тяжести действуют сосредоточенная сила F, подвешенный груз веса Р, пара сил с моментом М и равномерно распределенная нагрузка интенсивности q.
Определить: положение центра тяжести тела ADB (точка С с координатами (хс,ус), в которой приложен вес тела G); реакции опор; давление в соединительном шарнире В (Рис. С2.1, табл. "Исходные данные").
Рис. С2.1

Табл. "Исходные данные"
Задача К1. Плоское движение тела
Условие. Плоский механизм состоит из стержней и соединенных друг с другом и с неподвижными опорами шарнирами. Длины стержней AB =80 см, OA =40 см. Кривошип ОА вращается с угловой скоростью ωОА=2,5 рад/с против часовой стрелки.
Для заданного положения механизма найти:
1. Скорости и ускорения точек А,В и С - νА, νВ, νС, аА, аВ, аС.
2. Угловые скорости ωОА, ωАВ и угловые ускорения εОА, εАВ всех звеньев механизма. Мгновенный центр скоростей РАВ и векторы скоростей точек изобразить на схеме механизма (Рис. К1.1)

Рис. К.1.1
Задача К2. Сложное движение точки
Плоская фигура D вращается вокруг неподвижной оси, проходящей через точку O1 перпендикулярно плоскости рисунка. Вращение фигуры задано уравнением: φпер(t)=2t-3t2 (φ - в радианах, t - в секундах).
По фигуре D по окружности радиуса R=40 см движется точка М. Закон ее относительного движения ![]() (φ - в радианах, t - в секундах).
(φ - в радианах, t - в секундах).
Определить абсолютную скорость и ускорение точки М в момент времени t=1c и изобразить полученные векторы скорости и ускорения на рисунке (Рис. К.1.2).

Рис. К.1.2
Задача Д1. Динамика точки
Условие. Тело S, рассматриваемое как материальная точка массы m=4кг движется по шероховатой поверхности из состояния покоя от точки А к точке В, в которой отрывается от поверхности и продолжает движение до точки К. На участке АВ, коэффициент трения на котором равен f=0,2, на тело действует постоянная сила Q=130H. Используя уравнение движения тела на участках АВ, ВК, основные теоремы динамики точки определить время движения от начального к конечному положению, т.е. от точки А к точке К, скорость тела в точке В, расстояние DK (Рис. Д.1.1).

Рис. Д.1.1
Задача Д2. Теорема о движении центра масс системы. Теорема об изменении кинетической энергии системы
Условие. Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1=18 кг, движущейся вдоль горизонтальных направляющих, и груза D массой m2=6 кг. В момент времени t0=0, когда скорость плиты u0=2 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты.
Желоб КЕ прямолинейный и при движении груза расстояние s=AD изменяется по закону ![]() , где s выражено в метрах, t - в секундах.
, где s выражено в метрах, t - в секундах.
Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить величину полной нормальной реакции направляющих N1 в момент времени t1=1 c (Рис. Д.2.1)

Рис. Д.2.1
Задача ДЗ. Теорема об изменении кинетического момента системы
Условие. Однородная горизонтальная платформа (со сторонами R и 2R, где R=1,2 м) массой m1=24 кг вращается с угловой скоростью ω0=10 с-1 вокруг вертикальной оси z, отстоящей от центра масс С платформы на расстоянии ОС=b=R.
В момент времени t0=0 по желобу платформы, начинает двигаться (под действием внутренних сил) груз D массой m=8 кг по закону s=0,4t3, где s выражено в метрах, t - в секундах. Одновременно на платформу, начинает действовать пара сил с моментом М=-6t2 (задан в ньютон-метрах; при М<0 его направление противоположно показанному на рисунке).
Определить зависимость ω=f(t), т. е. угловую скорость платформы, как функцию времени (Рис. Д.3.1)

Рис. Д.3.1
Цена: 2000 руб.
Расчетно-графическое задание №1 по статике; 6 стр.
Дано:

Во всех вариантах заданий принять: Р2=10Н; Р=Р′=Р1
№ п/п | Р1(Н) | qmax (Н/м) | q (Н/м) | М (Н·м) | а (м) | КЕ (м) | α° | γ° |
| 1 | 1,5 | 1,0 | 4,8 | 1,0 | 1,2 | 0,6 | 60 | 45 |
Определить:
RAX(β), RAY(β), RA(β), RCX(β), RCY(β), RC(β), RB(β), MA(β).
Цена: 300 руб.
Расчетно-графическое задание №2 по статике; 10 стр.
Задача 1
По данным уравнениям движения точки М установить вид ее траектории и для момента времени t1 найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в данной точке.
| 14 | x= -2t - 2 (м); y = 2 + 4t (м) | 1,0 |
Задача №2
| № варианта | Радиусы шкивов 2 и 3, м | Начальные условия | Координаты груза 1 при t=t2 | Заданный момент времени | |||||
| R2 | r2 | R3 | r3 | х0, м | V0, м/с | t2, c | x2, м | t1, c | |
| 13 | 0,60 | 0,40 | 0,80 | - | 0,07 | 0,08 | 5 | 5,57 | 2 |

ДАНО. Заданный механизм представлен на рисунке, уравнение движения груза 1 описывается выражением:
x=C2t2+C1t+C0
В начальный момент времени t0=0 начальная координата груза x0=0,07 м, а начальная скорость v0=0,08 м/с.
В момент времени t=t2=5с координата груза х2 = 5,57 м.
R2=0.60м; г2=0.4м; R3=0.8 м.
ОПРЕДЕЛИТЬ:
- уравнение движения груза 1 – x=x(t):
- скорость V1 и ускорение a1 груза 1 в момент времени t = t1;
- угловые скорости ω2 и ω3 и угловые ускорения ε2 и ε3 шкивов 2 и 3 в момент времени t = t1;
- скорость VМ и ускорение aМ точки М шкива 3 при t=t1.
Цена: 600 руб.
Контрольная работа по инженерной и компьютерной графике (1 вариант); 5 чертежей
Задание №1. Плоские сечения поверхностей. Построение трех изображений геометрического тела с вырезом
Краткие методические рекомендации
Содержание.
Построить три проекции сферы со сквозным отверстием.
Оформление.
Формат А3. На формате вычертить рамку с отступом от левого края листа 20 мм, от остальных - по 5 мм. Основную надпись не выполнять. В нижней части справа шрифтом 5 (ГОСТ 2.304 – 81) написать номер варианта, фамилию, инициалы. Основание букв должно отстоять от рамки листа на 10 мм.
Построение условия.
Построение условия (фронтальная и горизонтальная проекции) выполняется по точкам. Координаты точек известны и приведены в таблице 1.2 :
О - центр сферы;
R - радиус сферы;
А, В, С, D - четырехугольный вырез.

Начало координат выбрать в середине листа и вычертить оси координат.
Пример построения условия приведен на рисунке 1.31.
Пример решения задачи - рисунок 1.32.

Читать подробнее
Пример решения задачи и краткие методические рекомендации
Задачу "Тело с отверстием" следует решать по определенной методике.
1) Продолжить все заданные плоскости, формирующие вырез, до полного пересечения с поверхностью.
2) Определить форму сечения от каждой секущей плоскости. В примере таких плоскостей четыре. Во всех четырех случаях сечение - окружность. Но от наклонной плоскости, проходящей по линии А2В2, горизонтальная и профильная проекции окружности - эллипсы; от других плоскостей окружности проецируются без искажения.
3) Далее задача сводится к теме "Плоские сечения".
Следует решать задачу по действиям, последовательно рассматривая каждую плоскость. При этом сечение необходимо строить полностью, оставляя за пределами выреза его контур в тонких линиях.
Построение наклонного сечения сферы подробно разобрано в примере 2 (п.1.3.3.5), а построение окружностей не вызывает затруднений.
Обводка линий должна соответствовать требованиям ГОСТ 2.303 – 68. Типы линий приведены в таблице 1.4.

Задание №2. Взаимное пересечение поверхностей. Построение линии пересечения двух поверхностей вращения.
Пример и краткие методические рекомендации
Содержание.
Построить две проекции линии пересечения поверхностей вращения.
Оформление.
Формат А3. На формате вычертить рамку без основной надписи с отступом от левого края листа 20 мм. Короткую сторону листа при этом расположить горизонтально. В нижней части справа шрифтом 5 написать номер варианта, фамилию и инициалы. Основание букв должно отстоять от рамки листа на 10мм.
Построение условия.
Построение условия выполняется по точкам. Координаты точек приведены в таблице 1.3. Начало координат следует выбрать в правой части листа, вычертить координатные оси.

При построении условия по координатам взаимное расположение поверхностей может отличаться от условия в примере.
Пример решения - рисунок 1.41.

Краткие методические рекомендации.
1) Заданы конус и цилиндр. Цилиндр расположен так, что его ось перпендикулярна фронтальной плоскости проекций. Поэтому боковая поверхность цилиндра проецируется на фронтальную плоскость в виде одной линии – окружности. Фронтальная проекция линии пересечения будет совпадать с этой окружностью.
2) Точки линии пересечения следует строить по алгоритму – п.1.4.5.
3) При построении применить способ вспомогательных секущих плоскостей.
4) Обратить внимание на обводку задачи, учитывая, что одна поверхность может закрывать другую.
При построении проекций линии пересечения необходимо контролировать область нахождения точек. Точки должны находиться на “площади наложения” проекций пересекающихся поверхностей. На рисунке 1.42 заштрихована площадь наложения наклонного цилиндра и эллипсоида.

Задание №3. Изображения на чертежах: виды, разрезы, сечения. Построение трех изображений детали по двум заданным с выполнением полезных разрезов и наклонного сечения.
Краткие методические рекомендации.
По двум заданным видам построить три изображения,
Выполнить заданные разрезы и наклонное сечение.
Нанести размерные линии.
Варианты задания приведены в приложении А.

Изучить:
- Заданные виды
- Материал раздела 2
- Настоящие рекомендации
Рекомендуемая последовательность выполнения листа 3
Лист формата А3 оформить рамкой и основной надписью по форме 1.
Можно использовать формат с типографским оформлением, если оно соответствует действующим ГОСТам.
Информация о форматах и основных надписях - приложение Б.

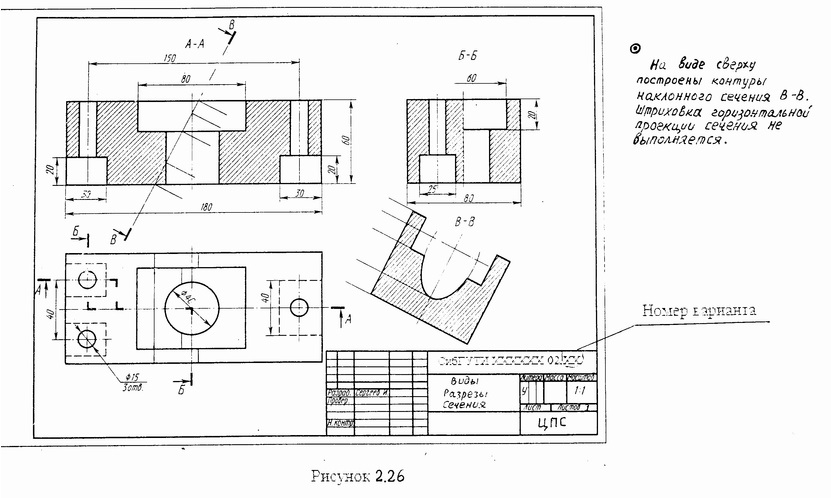
Оформление основной надписи на листе 3 – рисунок 2.26.

Перечертить заданные виды в натуральном масштабе и построить вид слева.
Информация о масштабах - приложение Б.

Выполнить заданные разрезы.
Построить наклонное сечение. Для этого:
- Построить тонкими линиями наложенную проекцию наклонного сечения на виде сверху.
- На свободном поле чертежа в прямой (или непрямой) проекционной связи построить натуральную величину наклонного сечения.
- Обратитесь к разделу 1, п.1.5.2, задача 3.
- Все линии построения сохранить.
Помощь в решении этой задачи окажут рисунки 1.52, 1.53 (раздел 1) и пример выполнения листа 3 контрольной работы на рисунке 2.26.

Нанести размеры, распределив их между тремя изображениями.
При этом размеры внешние следует отнести к видам, а размеры внутренних элементов – к разрезам. Некоторые правила нанесения размеров в соответствии с требованиями ГОСТ 2.307-68 приведены в приложении В.


Выполнить обводку чертежа линиями, установленными ГОСТ 2.303-68 .
Типы линий и их назначение приведены в приложении Г.

Все надписи (текстовые или цифровые ) выполнить шрифтом 3,5 или 5 в соответствии с ГОСТ 2.304 – 81. Примеры написания букв и цифр русского и латинского алфавитов приведены в приложении Д.


Перечень действующих Государственных стандартов Единой системы конструкторской документации приведен в приложении Е.
Литература
А.А.Чекмарев. Начертательная геометрия и черчение. Учебник для вузов. – Санкт-Петербург: ВЛАДОС, 1999. – 471с.
Государственные стандарты ЕСКД.
ПРИЛОЖЕНИЕ Е (справочное)
Перечень действующих государственных стандартов Единой системы конструкторской документации
ГОСТ 2.104-68. Основные надписи.
ГОСТ 2.301-68. Форматы.
ГОСТ 2.302-68. Масштабы.
ГОСТ 2.303-68. Линии.
ГОСТ 2.304-81. Шрифты чертежные.
ГОСТ 2.306-68. Обозначения графические материалов и правила их нанесения на чертежах.
ГОСТ 2.307-68. Нанесение размеров и предельных отклонений.
ГОСТ 2.317-69. Аксонометрические проекции.
ГОСТ 2.321-84. Буквенные обозначения на чертежах.
ГОСТ 2.701-84. Схемы. Виды и типы. Общие требования к выполнению.
ГОСТ 2.708-81. Правила выполнения электрических схем цифровой вычислительной техники. ГОСТ 2.710-81. Обозначения буквенно-цифровые в электрических схемах.
ГОСТ 2.721-74. Обозначения общего применения.
Обозначения условные графические в электрических схемах:
ГОСТ 2.723-68. Катушки индуктивности, дроссели, трансформаторы, автотрансформаторы, магнитные усилители.
ГОСТ 2.728-74. Резисторы, конденсаторы.
ГОСТ 2.729-68. Приборы электроизмерительные.
ГОСТ 2.730-73. Приборы полупроводниковые.
ГОСТ 2.735-68. Антенны.
ГОСТ 2.741-68. Приборы акустические.
ГОСТ 2.743-91. Элементы цифровой техники.
ГОСТ 2.746-68. Квантовые генераторы и усилители.
ГОСТ 2.751-73. Электрические связи, провода, кабели и шины.
ГОСТ 2.752-71. Устройства телемеханики.
ГОСТ 2.757-81. Устройства коммутационные и контактные соединения.
ГОСТ 2.759-82. Элементы аналоговой техники.
Задание №4 и №5. Схема электрическая структурная. Схема электрическая принципиальная.
1. Цель задания – изучить правила выполнения и оформления электрических структурных и принципиальных схем по ГОСТ 2.701-84 и 2.702-75.
2. В вариантах заданий все функциональные группы и элементы схем заданы окружностями. Технические данные элементов и наименования функциональных групп сведены в таблицы. Необходимо подобрать условные графические обозначения по соответствующим ГОСТ ЕСКД или по таблицам 1 и 2 в приложениях.


Начертить условные графические обозначения вместо окружностей, при этом линии электрических связей сохранить.
- Обозначить элементы схем в соответствии с требованиями ГОСТ 2.701-84 и 2.702-75.
- Выполнить перечень элементов для принципиальной схемы.
- Заполнить основную надпись в соответствии с ГОСТ 2.104-68 и 2.701-84.
Примеры выполнения заданий даны на рисунках 3.11, 3.12, 3.13, 3.14.

 ]
]


3. Задание выполняется на двух форматах А3 (297х420)мм по индивидуальным вариантам, которые прилагаются.
Задания на электрические структурные схемы даны в (приложении Б), на электрические принципиальные схемы – в (приложении В).


ЛИТЕРАТУРА
Стандарты ЕСКД по состоянию на 1.01.91г.
Усатенко С.Т., Коченюк Т.К., Терехова М. В. Выполнение электрических схем по ЕСКД.-М.: Издательство стандартов, 1989.
Свернуть текст
Цена: 500 руб.
Контрольная работа по сопротивлению материалов; 34 стр.
ЗАДАЧА №1
Ступенчатый брус нагружен силами Р1, Р2 и Р3, направленными вдоль его оси. Заданы длины участков a, b, c и площади их поперечных сечений F1 и F2. Модуль упругости материала Е=2·105 МПа, предел текучести σт=240 МПа и запас прочности по отношению к пределу текучести nт=1,5.

Расчетная схема к задаче №1
Требуется:
1) построить эпюры продольных сил N, напряжений σ и продольных перемещений Δ;
2) проверить, выполняется ли условие прочности.
ЗАДАЧА №2
Абсолютно жёсткий брус АВ опирается на шарнирно-неподвижную опору и прикреплен с помощью шарниров к двум стальным стержням.

Расчетная схема к задаче №2
Требуется подобрать сечения стержней по условию их прочности, приняв запас прочности по отношению к пределу текучести nт=2,5.
Соотношение площадей поперечных сечений стержней указано на расчетных схемах, модуль упругости стали для всех вариантов Е=2·105 МПа.
Студенты строительных специальностей дополнительно определяют допускаемую силу, используя расчет по предельной грузоподъемности, и сравнивают ее с заданной.
Р = 5кН, a = 1,2 м, b = 1,5 м, c = 0,8 м, Сталь 30, σт = 300 МПА
ЗАДАЧА №3
К стальному брусу круглого поперечного сечения приложены четыре крутящих момента М1, М2, М3, Х три из которых известны.
Требуется:
1) установить, при каком значении момента Х угол поворота правого концевого сечения равен нулю;
2) при найденном значении Х построить эпюру крутящих моментов;
3) при заданном значении допускаемого напряжения [τ] определить диаметр вала из условия его прочности и округлить величину диаметра до ближайшей большей стандартной величины, равной 30, 35, 40, 45, 50, 60, 80, 90, 100 мм;
4) проверить, выполняется ли условие жесткости бруса при выбранном диаметре, если допускаемый угол закручивания [θ] = 1 град/м;
5) построить эпюру углов закручивания.
Для всех вариантов принять модуль сдвига для стали G=8·105 МПа
a = 0,6 м, b = 0,5 м, М1 = 1,8 кН·м, М2 = 1,7 кН·м, М3 = 1,2 кН·м, [τ] = 40 МПа

Расчетная схема к задаче №3
ЗАДАЧА №4
Для двух заданных сечений, состоящих из нескольких элементов или имеющих вырезы, определить положение главных центральных осей инерции и вычислить величины моментов инерции относительно этих осей.

Расчетная схема к задаче №4 (для первого сечения)
Профиль прокатный: полоса 180×10, уголок 75×50×6
Расчетная схема к задаче №4 (для второго сечения)
а=20 см
ЗАДАЧА №5
Для заданных схем балок требуется:
Построить эпюры поперечных сил и изгибающих моментов; подобрать поперечные сечения балок по следующим вариантам:
а) для стальной балки (рис.11,а) - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b=2; круглое - диаметром d;
б) для чугунной балки (рис.11,б) - форму сечения выбрать по рис.12, определить размеры сечения из условия прочности по допускаемым напряжениям;
в) для стальной балки (рис.11,в) - сечение, состоящее из двух швеллеров.
P1 = 45 кН, Р2 = 80 кН, m1 = 12 кН·м, m2 = 10 кН·м, a=1,5 м, q=15 кН/м
Допускаемое напряжение для стали [σ],













